Embedding Krzysztof in the plane
This note is dedicated to Krzysztof, with precious memories of four decades of countably many meetings, uncountable many conversations about logic, mathematics, theory, taxes, life and math and logic puzzles. First in Utrecht around 1975 at the Mathematisch Instituut, then as near neighbours at Mathematisch Centrum-CWI, and the last few years after Krzysztof’s Asian Adventures in our regular Basket lunches on the VU campus, to share the latest interesting books, recent academic news and more puzzles, like the chess problem of Guarini.

This note offers Krzysztof an elaboration of a rather well-known puzzle, namely how many times certain figures such as the 8 or the Y can be embedded in the plane. The figures can be copied as many times we want, and we can scale them to any size by any multiplication factor. But they must be placed in the plane without overlapping each other. The question is whether they can countably many times embedded, or even uncountable many times. There are several proofs that the figure 8 can only countably often embedded; and likewise the figure Y.
Consideration of these questions goes back at least to 1928, in the topological paper by R. L. Moore: Concerning triods in the plane and the junction points of plane continua, Proc Natl Acad Sci U S A. Jan 1928; 14(1): 85–88. The present proof appears in a math forum http://mathoverflow.net/questions/27244/how-many-tacks-fit-in-the-plane, and is due to Greg Kuperberg, June 2010, and is a marvel of succinctness. The major role in the proof is played by an infinitary Pigeon Hole Principle, stating that among countably many pigeon holes containing together uncountably many pigeons, there must be at least one pigeon hole containing again uncountably many pigeons.
For the present occasion there are two questions:
- How many times can the (disconnected) figure KRZYSZTOF be embedded in the plane?
- Same question for each of the separate letters of KRZYSZTOF.
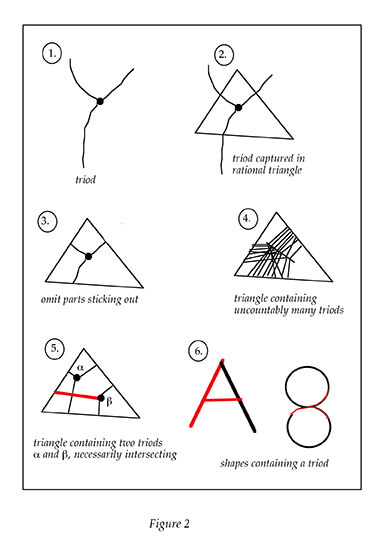
Following Moore, we call a ’triod’ any figure consisting of a junction point where three line segments, or pieces of continuous curves, are glued together, such as in the letter Y. An easy generalization is to replace ‘three’ by any finite number. e.g. the figure ‘+’ would be a 4-od, and the proof below works as well. Here it is: Suppose we have embedded uncountably many triods in the plane. See Figure 2. Now we capture every triod (1) in a rational triangle (2) meaning that the junction the point is inside the triangle every side of the triangle is intersected by precisely one leg. The triangle is called rational if its three coordinate points have rational coordinates. Next, we erase the parts of the three legs that stick out of the triangle (3). Clearly there are countably many rational triangles only. Hence by the appropriate infinitary version of the pigeonhole principle we have at least one triangle capturing uncountably many triods (4). A fortiori we have a triangle containing two triods α and β (5). However, by topological properties of the plane, these triods must necessarily intersect; see Figure 2 (5). We can conclude that only countably many triods can be embedded. Figure 2 (6) contains some shapes that contain a triod; clearly for such shapes it also
holds that they can only be embedded countably in the plane. For the letters of the alphabet we can use this argument to deal with A , B , E , F , H , K , P , Q , R , T , X , Y and for the digits 4 , 6 , 8 , 9 . For the 8 there is a well-known easier argument consisting of picking a rational point in each of the two halves. There are only countably many of such pairs and two identical pairs cannot be shared by two disjoint copies of 8. So what remains for Krzysztof to brood over? I guess the letter S. The problem seems to be what exact shape it has; two half circles glued together is easy, but many S’s are not that simple. So Krzysztof, enjoy this remaining puzzle and in particular, your pension time! Now you get around to your real work.