Braids are a fascinating subject in mathematics in several areas, also in term rewriting.
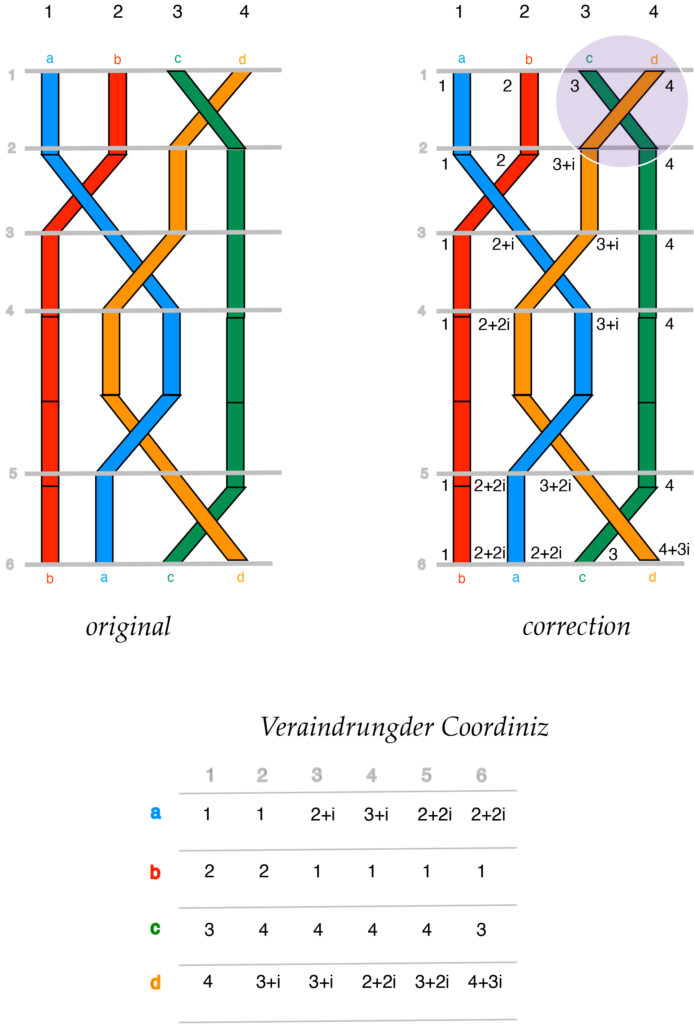
In a history research visit of topologist Joseph Przytycki in the library of Gottingen University he discovered in one of the Notebooks of Carl Friedrich Gauss a sketch of a braid together with a table giving the spatial coordinates of the strands of the braid, with a use of complex numbers to describe whether a strand was going down or up or staying on the same level. But Joseph noticed that Gauss was a bit sloppy in his notation of the coordinates, which made it puzzling what he actually meant. A scrutiny of the figure of Gauss gave us recently an aha-insight how to very plausibly correct what part of the figure. The Prince of Mathematicians made only one ‘over and under’ mistake’, as displayed in our figure, in the purple disc. So, Gauss was indeed already contemplating braids, a century before Emil Artin put this notion under his reseach microscope and and in his seminal article on the mathematical map. Joseph Przytycki informed us in personal email contact that Gauss in fact anticipated what experts now would call
‘configuration spaces’.
In fact, come to think of it, one and a half century later another of our heroes, Alan Turing, contemplated a somewhat similar spatial rendering of the generalisation of braids, namely of knots. He proposed to treat knots in the way of string rewriting, and wrote a beautiful essay about string rewriting as a general model of computation.